Exercice Corrigé Ordonnancement Des Processus – Partie 4

L‘ordonnancement du processus est à la base des systèmes d’exploitation multiprogrammés. En répartissant l’unité centrale entre les processus, le système d’exploitation peut rendre l’ordinateur plus productif. Dans ce chapitre, nous présentons des exercices corrigés sur les concepts de base de l’ordonnancement, l’idée d’allocation de ressources et discutons en détail de l’ordonnancement de l’unité centrale. FCFS, SJF, Round-Robin, Priorité et les autres algorithmes d’ordonnancement devraient être familiers à vous.

Exercice 1: Pourcentage d’inactivité du CPU

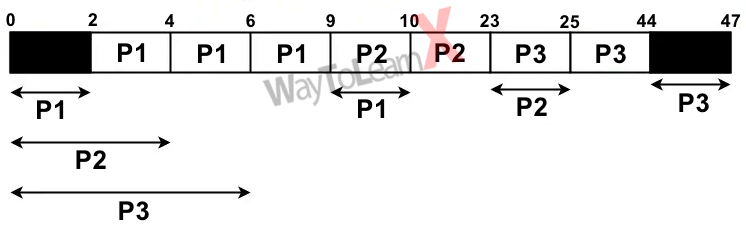
Considérons trois processus, arrivant tous au temps zéro, avec un temps d’exécution total de 10, 20 et 30 unités respectivement. Chaque processus passe les premiers 20 % de son temps d’exécution à faire des E/S, les 70 % suivants à faire des calculs et les derniers 10 % à refaire des E/S. Le système d’exploitation utilise un algorithme d’ordonnancement basé sur l’algorithme d’ordonnancement Shortest Remaining Time First (SRTF) et planifie un nouveau processus soit lorsque le processus en cours est bloqué sur les E/S, soit lorsque le processus en cours termine sa rafale de calcul. Supposons que toutes les opérations d’E/S puissent se chevaucher autant que possible. Quel est le pourcentage d’inactivité de l’unité centrale (CPU) ?

A 0%

B 10.6%

C 30.0%

D 89.4%

B

D’après la question, nous avons:

Rafale = Temps d’exécution

+--------------+------------------+------------+------------+------------+
|              | Totale du Rafale | Rafale E/S | Rafale CPU | Rafale E/S |
+--------------+------------------+------------+------------+------------+
| Processus P1 | 10               | 2          | 7          | 1          |
+--------------+------------------+------------+------------+------------+
| Processus P2 | 20               | 4          | 14         | 2          |
+--------------+------------------+------------+------------+------------+
| Processus P3 | 30               | 6          | 21         | 3          |
+--------------+------------------+------------+------------+------------+

L’algorithme d’ordonnancement utilisé est celui du SRTF « plus court temps restant en premier ».

Pourcentage de temps d’inactivité de l’unité centrale (CPU)
= (5 / 47) x 100
= 10.638%
L’option correcte est donc (B).

 

Exercice 2: SRTF « plus court temps restant en premier »

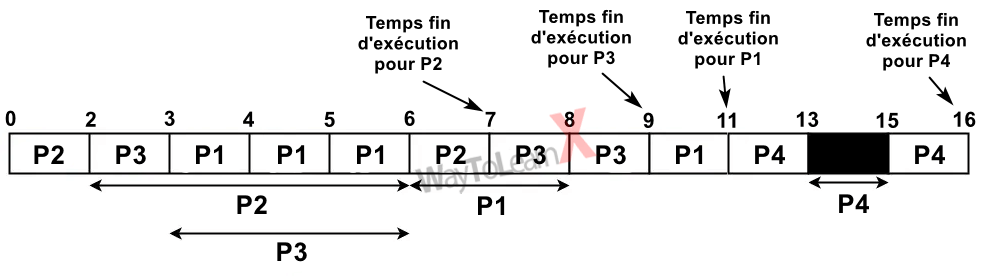
Considérons les 4 processus suivants avec un temps de rafale (temps d’exécution). Dessinez l’ordre d’exécution des processus à l’aide d’un diagramme de Gantt (ligne temporelle) en utilisant l’algorithme d’ordonnancement SRTF « plus court temps restant en premier », et calculez le temps d’attente moyen et le temps moyen de rotation.

+-----------+-----------------+--------------------------------------+
| Processus | Temps d'arrivée |           Temps de rafale            |
|           |                 |------------+------------+------------+
|           |                 | Rafale E/S | Rafale CPU | Rafale E/S |
+-----------+-----------------+------------+------------+------------+
| P1        | 0               | 3          | 2          | 2          |
+-----------+-----------------+------------+------------+------------+
| P2        | 0               | 2          | 4          | 1          |
+-----------+-----------------+------------+------------+------------+
| P3        | 2               | 1          | 3          | 2          |
+-----------+-----------------+------------+------------+------------+
| P4        | 5               | 2          | 2          | 1          |
+-----------+-----------------+------------+------------+------------+

Maintenant, on sait que:

Temps de rotation = Temps fin d’exécution – Temps d’arrivée

Temps d’attente = Temps de rotation – Temps de rafale

+-----------+-----------------+-------------------+
| Processus | Temps d'attente | Temps de rotation |
+-----------+-----------------+-------------------+
| P1        | 11 – (3+2) = 6  | 11 – 0 = 11       |
+-----------+-----------------+-------------------+
| P2        | 7 – (2+1) = 4   | 7 – 0 = 7         |
+-----------+-----------------+-------------------+
| P3        | 7 – (1+2) = 4   | 9 – 2 = 7         |
+-----------+-----------------+-------------------+
| P4        | 11 – (2+1) = 8  | 16 – 5 = 11       |
+-----------+-----------------+-------------------+

Temps moyen d'attente = (Temps d'attente total) / (Nombre total de processus) 
                      = (6 + 4 + 4 + 8) / 4
                      = 22 / 4
                      = 5.5 unités
					  
Temps moyen de rotation = (Temps de rotation total) / (Nombre total de processus) 
                        = (11 + 7 + 7 + 11) / 4
                        = 36 / 4
                        = 9 unités

Exercice 3: Ordonnancement par priorité (Priority Scheduling)

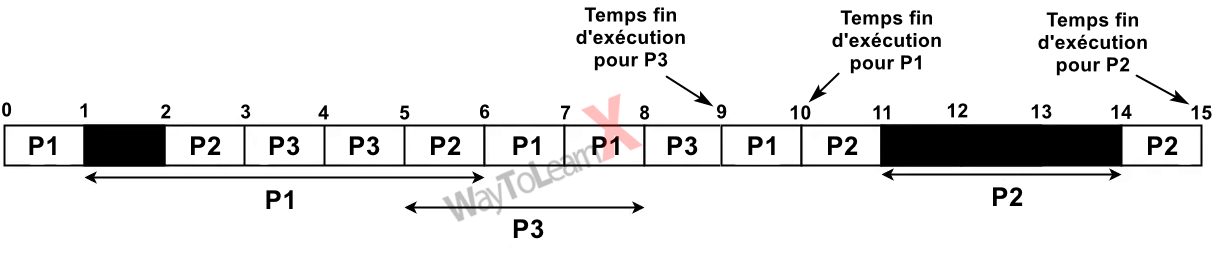
Considérons les 3 processus suivants avec un temps de rafale (temps d’exécution). Dessinez l’ordre d’exécution des processus à l’aide d’un diagramme de Gantt (ligne temporelle) en utilisant l’algorithme d’ordonnancement par priorité, et calculez le temps d’attente moyen et le temps moyen de rotation. (Un chiffre plus bas signifie une priorité plus élevée).

+-----------+-----------+----------+--------------------------------------+
| Processus | Temps     | Priorité |            Temps de rafale           |
|           | d'arrivée |          |------------+------------+------------+
|           |           |          | Rafale E/S | Rafale CPU | Rafale E/S |
+-----------+-----------+----------+--------------------------------------+
| P1        | 0         | 2        | 1          | 5          | 3          |
+-----------+-----------+----------+--------------------------------------+
| P2        | 2         | 3        | 3          | 3          | 1          |
+-----------+-----------+----------+--------------------------------------+
| P3        | 3         | 1        | 2          | 3          | 1          |
+-----------+-----------+----------+------------+------------+------------+

Maintenant, on sait que:

Temps de rotation = Temps fin d’exécution – Temps d’arrivée

Temps d’attente = Temps de rotation – Temps de rafale

+-----------+-----------------+-------------------+
| Processus | Temps d'attente | Temps de rotation |
+-----------+-----------------+-------------------+
| P1        | 10 – (1+3) = 6  | 10 – 0 = 10       |
+-----------+-----------------+-------------------+
| P2        | 13 – (3+1) = 9  | 15 – 2 = 13       |
+-----------+-----------------+-------------------+
| P3        | 6 – (2+1) = 3   | 9 – 3 = 6         |
+-----------+-----------------+-------------------+

Temps moyen d'attente = (Temps d'attente total) / (Nombre total de processus) 
                      = (6 + 9 + 3) / 3
                      = 18 / 3
                      = 6 unités
					  
Temps moyen de rotation = (Temps de rotation total) / (Nombre total de processus) 
                        = (10 + 13 + 6) / 3
                        = 29 / 3
                        = 9.67 unités

Exercice 4:

Un algorithme d’ordonnancement du CPU détermine l’ordre d’exécution des processus programmés. Étant donné que n processus doivent être ordonnancés sur un processeur, combien y a-t-il d’ordonnances différentes possibles ? Donnez une formule en fonction de n.

Exercice 5:

Considérons les 6 processus suivants avec un temps de rafale (temps d’exécution). Dessinez l’ordre d’exécution des processus à l’aide d’un diagramme de Gantt (ligne temporelle). Si la politique d’ordonnancement du CPU est First Come First Serve (FCFS) et qu’il y a une unité du temps d’attente pour le changement de contexte dans l’ordonnancement des processus, déterminez l’efficacité de l’algorithme.

+-----------------+-----------------+-----------------+
| ID du processus | Temps d'arrivée | Temps de rafale |
+-----------------+-----------------+-----------------+
| P1              | 0               | 3               |
+-----------------+-----------------+-----------------+
| P2              | 1               | 2               |
+-----------------+-----------------+-----------------+
| P3              | 2               | 1               |
+-----------------+-----------------+-----------------+
| P4              | 3               | 4               |
+-----------------+-----------------+-----------------+
| P5              | 4               | 5               |
+-----------------+-----------------+-----------------+
| P6              | 5               | 2               |
+-----------------+-----------------+-----------------+

Ici, δ représente le temps d’attente pour le changement de contexte.
Maintenant,
Temps inutile / Temps perdu = 6 x δ = 6 x 1 = 6 unités
Temps total = 23 unités
Temps utile = 23 unités – 6 unités = 17 unités

Efficacité (η)
= Temps utile / Total Total
= 17 unités / 23 unités
= 0.7391
= 73.91%