Exercices Corrigés Dépendances fonctionnelles(Forme Normale) – Partie 6
La meilleure façon d’apprendre quelque chose est de pratiquer des exercices. Nous avons préparer ces exercices corrigés pour les personnes (débutantes ou intermédiaires) qui sont familières avec les dépendances fonctionnelles et normalisation des bases de données. Nous espérons que ces exercices vous aideront à améliorer vos compétences sur les Dépendances fonctionnelles et Normalisation. Les exercices corrigés suivantes sont actuellement disponibles, nous travaillons dur pour ajouter plus d’exercices. Bon apprentissage!
Vous pouvez lire notre tutoriel sur les dépendances fonctionnelles et normalisation des bases de données avant de résoudre les exercices suivants.
Vous savez que la dépendance fonctionnelle A -> B signifie que B dépend de A, c’est-à-dire qu’à partir de la valeur de A, nous pouvons trouver la valeur de B dans la relation.
Donc, pour prouver que A -> B est valide dans une relation, l’une des conditions suivantes doit être vraie :
- Condition1 : toutes les valeurs de A doivent être uniques.
- Condition2 : toutes les valeurs de B doivent être identiques.
- Condition3 : Si deux ou plusieurs tuples de la relation ont la même valeur pour l’attribut A, alors il doit également y avoir la même valeur pour l’attribut B.
1. Étant donné la relation R=(A,B,C,D), trouvez si R est en 3NF ou BCNF par rapport aux DF suivantes (chaque question en chiffres est séparée):
1) B → C, C → A, C → D 2) ABC → D, D → A 3) A → C, B → D
1) B est la clé candidate et R n’est pas en 3NF
2) (A,B,C), (B,C,D) sont des clés candidates et R est en 3NF, mais pas en BCNF
3) (A,B) est la clé et R n’est pas en 3NF
2. Considérons une relation R=(A,B,C,D,E,F) qui satisfait les quatre DF suivantes :
AB → C, BC → AD, D → E, CF → B
AB → D est-il valide ? Si oui, donnez une preuve structurée; sinon, donnez un contre-exemple.
Oui, AB → D est valide. Voici une preuve :
1. AB → B Réflexivité 2. AB → BC union : 1 et DF1 3. AB → AD transitivité : 2 et DF2 4. AB → D décomposition : 3
Vous pouvez également calculer {A, B}+.
3. Étant donné une relation R(A,B,C,D,E,F,G) avec les cinq dépendances fonctionnelles F suivantes :
(1) A → BC (2) E → CF (3) B → E (4) CD → EF (5) A → G
3.1) Trouver la fermeture(clôture) de A
(6) A → B (puisque (1)) (7) A → C (puisque (1)) (8) A → E (propriété transitive (6) et (3)) (9) A → CF (propriété transitive de (8) et (2)) (10) A → G (puisque (5))
Donc, {A}+ = {A,B,C,E,F,G}
3.2) Trouver une clé candidate pour R.
La clé candidate pour R est: {A,D}.
3.3) Quelle est la fermeture de G ?
La fermeture de G est {G}+ = {G}
4. Étant donné une relation R(A,B,C,D,E,G) avec les huit dépendances fonctionnelles suivantes:
AB → C D → EG C → A BE → C BC → D CG → BD ACD → B CE → AG
Pour les affirmations suivantes, décidez si elles sont vraies ou fausses. Pour les affirmations fausses, expliquez pourquoi vous pensez qu’elles sont fausses.
4.1) La fermeture de BC est {A,D,E,G}
A VRAI
B FAUX
4.2) Tous les attributs de R sont dans la fermeture de BC.
A VRAI
B FAUX
4.3) La fermeture de AC est {A,C}.
A VRAI
B FAUX
4.4) ABC est une super clé de R.
A VRAI
B FAUX
4.5) ABC est une clé candidate de R.
A VRAI
B FAUX
4.6) BC est la seule clé candidate de R.
A VRAI
B FAUX
5. Considérons une base de données relationnelle sur les hôtels, les clients et leurs réservations, gérée par une société de réservation d’hôtels en ligne. La base de données se compose des tables suivantes (dont les clés primaires sont soulignées) :
Hôtel (hId, hNnom, hAdresse, hVille) Invité (iId, iNnom, iAdresse, iVille) Chambre (hid, numéroChambre, type, prix) Réservation (iId, hId, numéroChambre, dateDébut, année, nombreJours)
Où hId et iId sont les identifiants des hôtels et des clients, et la relation Réservation indique qu’un client a réservé une chambre d’hôtel pour un nombre spécifié de jours (nombreJours) à partir de dateDébut d’une année donnée. Par exemple, un tuple <1001, 5001, 350, Jan08, 2024, 7> dans Réservation indique que le client avec l’id ‘1001’ a réservé la chambre 350 de l’hôtel avec l’id 5001 pendant 7 jours à partir du 8 janvier 2024.
5.1) Ecrivez une expression d’algèbre relationnelle qui renvoie les identifiants des hôtels situés à Paris qui n’ont fait l’objet d’aucune réservation au cours de l’année 2024.
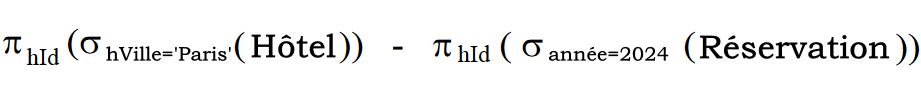
Tout hôtel ayant une réservation pour une année autre que 2024 sera inclus dans le résultat, même si le même hôtel a une autre réservation pour 2024!
5.2) Ecrire une expression d’algèbre relationnelle qui renvoie les identifiants des clients qui ont réservé au moins une chambre de type « Premium » dans chaque hôtel situé à Paris.
Ceci renvoie tous les clients qui ont réservé une chambre « Premium » dans un hôtel de Paris.
6. Considérons une relation R=(A,B,C). Pour chacune des règles suivantes, déterminez si elle est valide ou non. Si oui, donnez une preuve structurée; sinon, donnez un contre-exemple.
1) Si AB → C, alors A → C ? 2) Si AB → C, alors B → C ? 3) Si AB → C, alors (A → C) ou (B → C) ?
+---+---+---+ | A | B | C | +---+---+---+ | 1 | 1 | 1 | | 1 | 2 | 2 | +---+---+---+
2) Non valide, voici un contre-exemple :
+---+---+---+ | A | B | C | +---+---+---+ | 1 | 1 | 1 | | 2 | 1 | 2 | +---+---+---+
3) Non valide, voici un contre-exemple :
+---+---+---+ | A | B | C | +---+---+---+ | 1 | 1 | 1 | | 1 | 2 | 2 | | 2 | 1 | 2 | +---+---+---+
- Exercices Corrigés Dépendances fonctionnelles(Forme Normale) – Partie 1
- Exercices Corrigés Dépendances fonctionnelles(Forme Normale) – Partie 2
- Exercices Corrigés Dépendances fonctionnelles(Forme Normale) – Partie 3
- Exercices Corrigés Dépendances fonctionnelles(Forme Normale) – Partie 4
- Exercices Corrigés Dépendances fonctionnelles(Forme Normale) – Partie 5
- Exercices Corrigés Dépendances fonctionnelles(Forme Normale) – Partie 6
- Exercices Corrigés Dépendances fonctionnelles(Forme Normale) – Partie 7
